这是一篇 Neural Style Transfer 的简要介绍。一方面是我的学习笔记，另一方面想向大家介绍这种有趣的神经网络应用。
我不知道是否该翻译为「风格迁移神经网络」。但它的英文原名清晰地给出了3个信息：
Neural-神经 Style-风格 Transfer-传输/转换/迁移
这也是它最核心的3个属性。
Neural Style Transfer能做什么呢，就是学习一种图像的风格，然后把别的图像转换为这种风格。像下图所示：
看了HBO的《切尔诺贝利》迷你剧。其实有明显的歧视社会主义的色彩啦，解读方式不能不说是带有某种偏见。不过影响不大，毕竟令人震惊的事实就是无可撼动。
像武汉一样，切尔诺贝利核电站事故的第一瞬间，政府反应就是封城，切断外界联络。威权国家的这种思维惯性还是让人细思恐极。它总是轻易地牺牲掉一大群人。
这种理念跟西方的个体自由文化格格不入。可以想见，西方看待这次武汉，也跟看待切尔诺贝利一样——他们根本不相信你对外发布的信息，因为你的做法（封城）就不是一个符合他们价值观的行为。中国政府的操作已经把自己标榜到文化对立面，是不值得信任的。
近期我的PC遇到个问题，我的NS Pro手柄，在一段时间没有连接电脑后，再想连接时，无法顺利连接了。
具体来说，Pro手柄因为默认是Nintendo Switch的手柄，所以在插上NS后会自动配对连接。那么下次你想用它连接电脑蓝牙来玩PC游戏时，就需要重新配对了。
重新配对前，需要删掉前一次配对的信息，也就是在系统的显示蓝牙设备列表里，删掉Pro手柄的已配对项。
通常情况下这一切都很顺利，但这次遇到了bug：无法删除该蓝牙设备。
具体表现为：已配对项右下有删除键，可以点击，但点击之后无反应。
我check了网上能搜到的信息，包括微软官方这篇： https://answers.microsoft.com/zh-hans/windows/forum/all/win10%E8%93%9D%E7%89%99%E8%AE%BE%E5%A4%87%E6%97%A0/dd641a9b-ca95-491a-8cd9-90747b36fe2c
但微软的bug令人惊叹，相关注册表项禁止我修改，说我没有权限。我作为这台电脑的owner，却没有权限修改它。
最终找到的可行解决方案是这篇，转载其内容存档如下：
题记
Win10 很多 Bug
问题描述
Win10 与蓝牙设备（比如蓝牙键盘，蓝牙音箱）出现了无法连接的情况，本来打算删除已配对的设备，再重新配对连接。但 Win10 很多 Bug 呢，删除设备后重启蓝牙，那些原本被删除的设备又回来了，是的，全都回来了。
解决方法
尝试了很多方法，包括网上流传的打开飞行模式，在控制面板里的设备与打印机里删除设备等等，均无效。
后来的一切，是缘份了。和你恰好在浏览这篇文章道理相似。
原帖如下，链接：https://www.tenforums.com/drivers-hardware/22049-how-completely-remove-bluetooth-device-win-10-a.html
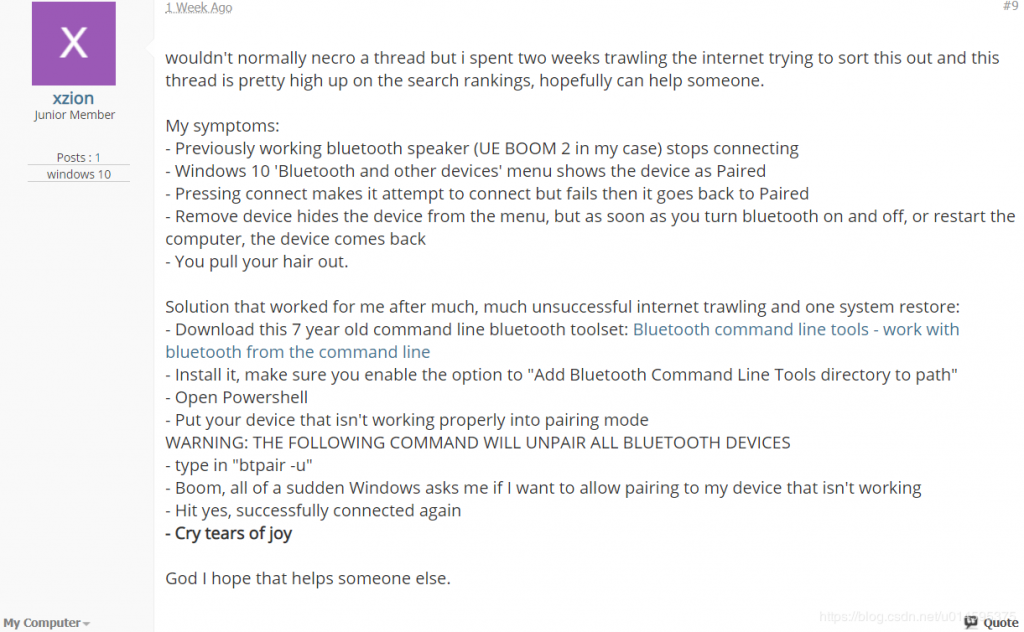
具体解决方法，翻译过来就是：
下载 修复工具，一路默认选项完成安装。防止链接失效，附上 百度网盘链接
打开 Powershell，命令行输入 btpair -u，回车执行
等待，会发现已配对的蓝牙设备 终于 成功 彻底 被删除了
喜极而泣
————————————————
版权声明：本文为CSDN博主「一木扶苏」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/u014595375/article/details/85730427
百度网盘下载连接备份如下：
链接: https://pan.baidu.com/s/1tghoYBZxkzxqwvxPYtVumg 提取码: si23
有段时间没写这种文章了。根据姜文电影的名场面，我决定将博客的这个栏目命名为——「正经人谁写日记呀」，哈哈。
2019年像之前的每一年一样，过得很快。对它的印象只剩加班加班、辞职家里蹲、旅行，然后，就是现在：手机在放歌，我坐在床上，敲打老旧的 MacBook，现在是 12.31 02:02。
又是不太长进的一年。原本没有值得写的东西。但今年有两个瞬间让我想写点什么：
一是前女友在微信上再次联络我之后，我觉得人和人也许是可以相互原谅的，心里稍微好受一点，当时感激地有写东西的冲动。
二是前几天，见了一些老朋友。看到大家都过得很好，也许说不上很好但也是「稳步前行」。似乎让我对自己也稍稍有了一点信心。
毕业后我在两个公司工作过，其中一家是台湾的电子制造公司LiteOn，第二家是华为。
这是一篇LiteOn领导拜托我写给他们介绍华为工程师生活的文章。我把它贴出来，作为对前东家讨论系列的第一篇，之后可能还会有别的分析文章。
表妹在大一的C语言课上写了个bug程序，发到群里让大家帮忙debug。我一眼看出其中存在一处“语法”错误：
if (0 < a < 10) {
…
}
一个很有意思的事是，我把它当成了“语法错误”，认为这样写根本编译不过。
但事实是，从之后的讨论中看到，这个程序没有编译失败。只是逻辑上有错而已——这个if后面的表达式永远为true。
我用gcc编译了一遍试试，报了这个warning：
warning: comparisons like ‘X<=Y<=Z’ do not have their mathematical meaning [-Wparentheses]
if (0 < a < 10) {
意味着我们一开始的判断是对的，0 < a < 10 确实不是正确的C语言写法，应该写作(0 < a) && (a < 10)。但编译器还是允许它通过了。程序运行时真正发生的是什么呢？：
（0 < a） < 10
相当于先执行了括号内的运算，返回 true 或 false。在C语言中 true == 1， false == 0。这两个值再去与10做比较。——当然是恒 <10 的，所以 (0 < a < 10) 这个表达式恒为 true，相关 if 语句永远不会走进 else 分支。
这方面的语法差异还挺有趣的，这篇文章里说，如果你没学过C，你可能会以为a < b < c就是a < b < c，如果你学过C，你会以为这里无法编译通过。
关于 a < b < c 的事实是
- 在 Python 里，
a < b < c的意思就是a < b < c - C语言里，编译能过，但有告警
comparisons like ‘X<=Y<=Z’ do not have their mathematical meaning - C++里，表现与C中相同，但还有个额外的告警，警告你在这个表达式中发生了布尔型与整型间的隐式转换
- Haskell里，这里会发生类型错误，因为 bool 和 int 之间没有隐式转换
- Fortran里，这是语法错误，因为
<符号没有关联性（non-associative (meaning operations cannot be chained, often because the output type is incompatible with the input types)）。
经验总结
在编译时开启所有编译告警，并尽可能地将它们清零，是一个好的习惯。
当然，也不是一概而论的。取决于你的项目性质，某些告警（未使用的函数、未使用的变量）还是可以选择关闭的。最好是开启所有告警，然后明确声明关闭特定的某几个告警；而不是直接关闭所有告警。
最近在思考关于哈希表二次探测再散列后如何查找的问题。暂时没找到解释。先转一篇有趣的科普文，以供后续研究。
原文来自： http://www.ruanyifeng.com/blog/2018/09/hash-collision-and-birthday-attack.html
一、哈希碰撞是什么？
所谓哈希（hash），就是将不同的输入映射成独一无二的、固定长度的值（又称”哈希值”）。它是最常见的软件运算之一。
如果不同的输入得到了同一个哈希值，就发生了”哈希碰撞”（collision）。
举例来说，很多网络服务会使用哈希函数，产生一个 token，标识用户的身份和权限。
AFGG2piXh0ht6dmXUxqv4nA1PU120r0yMAQhuc13i8
上面这个字符串就是一个哈希值。如果两个不同的用户，得到了同样的 token，就发生了哈希碰撞。服务器将把这两个用户视为同一个人，这意味着，用户 B 可以读取和更改用户 A 的信息，这无疑带来了很大的安全隐患。
黑客攻击的一种方法，就是设法制造”哈希碰撞”，然后入侵系统，窃取信息。
二、如何防止哈希碰撞？
防止哈希碰撞的最有效方法，就是扩大哈希值的取值空间。
16个二进制位的哈希值，产生碰撞的可能性是 65536 分之一。也就是说，如果有65537个用户，就一定会产生碰撞。哈希值的长度扩大到32个二进制位，碰撞的可能性就会下降到 4,294,967,296 分之一。
更长的哈希值意味着更大的存储空间、更多的计算，将影响性能和成本。开发者必须做出抉择，在安全与成本之间找到平衡。
下面就介绍，如何在满足安全要求的前提下，找出哈希值的最短长度。
三、生日攻击
哈希碰撞的概率取决于两个因素（假设哈希函数是可靠的，每个值的生成概率都相同）。
- 取值空间的大小（即哈希值的长度）
- 整个生命周期中，哈希值的计算次数
这个问题在数学上早有原型，叫做”生日问题“（birthday problem）：一个班级需要有多少人，才能保证每个同学的生日都不一样？
答案很出人意料。如果至少两个同学生日相同的概率不超过5%，那么这个班只能有7个人。事实上，一个23人的班级有50%的概率，至少两个同学生日相同；50人班级有97%的概率，70人的班级则是99.9%的概率（计算方法见后文）。
这意味着，如果哈希值的取值空间是365，只要计算23个哈希值，就有50%的可能产生碰撞。也就是说，哈希碰撞的可能性，远比想象的高。实际上，有一个近似的公式。
上面公式可以算出，50% 的哈希碰撞概率所需要的计算次数，N 表示哈希的取值空间。生日问题的 N 就是365，算出来是 23.9。这个公式告诉我们，哈希碰撞所需耗费的计算次数，跟取值空间的平方根是一个数量级。
这种利用哈希空间不足够大，而制造碰撞的攻击方法，就被称为生日攻击（birthday attack）。
四、数学推导
这一节给出生日攻击的数学推导。
至少两个人生日相同的概率，可以先算出所有人生日互不相同的概率，再用 1 减去这个概率。
我们把这个问题设想成，每个人排队依次进入一个房间。第一个进入房间的人，与房间里已有的人（0人），生日都不相同的概率是365/365；第二个进入房间的人，生日独一无二的概率是364/365；第三个人是363/365，以此类推。
因此，所有人的生日都不相同的概率，就是下面的公式。
上面公式的 n 表示进入房间的人数。可以看出，进入房间的人越多，生日互不相同的概率就越小。
这个公式可以推导成下面的形式。
那么，至少有两个人生日相同的概率，就是 1 减去上面的公式。
五、哈希碰撞的公式
上面的公式，可以进一步推导成一般性的、便于计算的形式。
根据泰勒公式，指数函数 ex 可以用多项式展开。
如果 x 是一个极小的值，那么上面的公式近似等于下面的形式。
现在把生日问题的1/365代入。
因此，生日问题的概率公式，变成下面这样。
假设 d 为取值空间（生日问题里是 365），就得到了一般化公式。
上面就是哈希碰撞概率的公式。
六、应用
上面的公式写成函数。
const calculate = (d, n) => {
const exponent = (-n * (n - 1)) / (2 * d)
return 1 - Math.E ** exponent;
}
calculate(365, 23) // 0.5000017521827107
calculate(365, 50) // 0.9651312540863107
calculate(365, 70) // 0.9986618113807388
一般来说，哈希值由大小写字母和阿拉伯数字构成，一共62个字符（10 + 26 + 26）。如果哈希值只有三个字符的长度（比如abc），取值空间就是 62 ^ 3 = 238,328，那么10000次计算导致的哈希碰撞概率是100%。
calculate(62 ** 3, 10000) // 1
哈希值的长度增加到5个字符（比如abcde），碰撞的概率就下降到5.3%。
calculate(62 ** 5, 10000) // 0.05310946204730993
现在有一家公司，它的 API 每秒会收到100万个请求，每个请求都会生成一个哈希值，假定这个 API 会使用10年。那么，大约一共会计算300万亿次哈希。能够接受的哈希碰撞概率是1000亿分之一（即每天发生一次哈希碰撞），请问哈希字符串最少需要多少个字符？
根据上面的公式倒推，就会知道哈希值的最短长度是22个字符（比如BwQ1W6soXkA1PU120r0yMA），计算过程略。
22个字符的哈希值，就能保证300万亿次计算里面，只有1000亿分之一的概率发生碰撞。常用的 SHA256 哈希函数产生的是64个字符的哈希值，每个字符的取值范围是0~9和a~f，发生碰撞的概率还要低得多。
七、参考链接
- How Long Should I Make My API Key?, by Sam Corcos
- Birthday problem, by Wikipedia
- Birthday attack, by Wikipedia
众所周知，Chrome的68版会将未使用 https 加密的网站标记为「不安全」。可以说 Google 是在不遗余力地推广传输层安全协议。
响应 Google 的号召。当我得知 https 证书也有一些免费版本可用时，就决定给自己的博客加上 https。
略过各种方案的比较和选择，这里直接记录（我认为）个人博客网站添加 https 证书的最佳实践：
不一定跟我一样，选择你自己的操作系统和服务器软件，certbot 页面上会提供对应的安装方法。
安装后继续按照 certbot 页面的说明 get start ，程序的交互式界面会引导你进行选择和配置。
跟随引导进行操作，完成后网站就被 Let’s Encrypt 提供的 SSL/TLS 证书保护起来了。是不是很有安全感！
服务器添加安全证书
我参考了这篇：Let’s Encrypt 给网站加 HTTPS 完全指南 但你不用按那篇文章里的步骤来，因为它已经是2年前的文章了，现在可是8102年，事情变得很简单： 只需在服务器上安装 certbot， 它自动帮你完成一系列的证书配置和验证操作。（需要对服务器有足够权限） 网址在：https://certbot.eff.org/ 我选择了 Apache on Ubuntu 16.04 (xenial) ，页面的提示如下：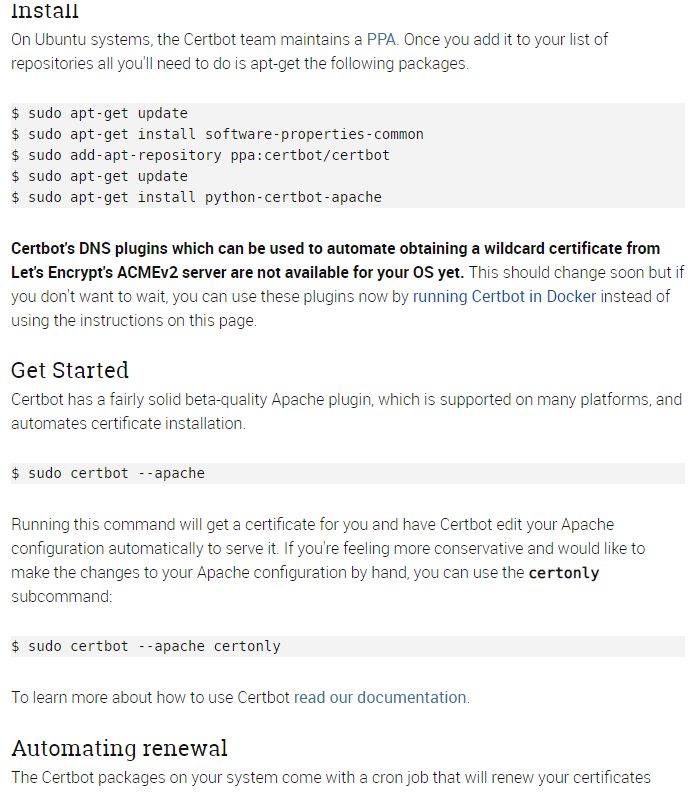
不一定跟我一样，选择你自己的操作系统和服务器软件，certbot 页面上会提供对应的安装方法。
安装后继续按照 certbot 页面的说明 get start ，程序的交互式界面会引导你进行选择和配置。
跟随引导进行操作，完成后网站就被 Let’s Encrypt 提供的 SSL/TLS 证书保护起来了。是不是很有安全感！
/etc/letsencrypt/renew/ 路径下找到。用下面这个命令测试自己的 renew 设置是否有效：
sudo certbot renew --dry-run一点清扫工作
现在你应该能通过前缀 https:// 的网址来访问自己的网站了。再回头试一下 http:// 访问，看会不会自动跳转到 https:// 。（如果没有，就要检查网站的重定向设置了） 不过，你也许会遇到，其他的 https 网站在浏览器里都有一把小绿锁显示，为什么我的网站只有小灰锁呢？ 在浏览器的小锁（或灰色叹号）上点击，可以看到它对网站潜在隐患的提示。 对于个人博客来说，问题通常出现在站内的图片和链接上。它们的地址可能不是 https 的，没有被 SSL/TLS 保护，所以会被中间人截获。YOUR_DOMAIN 为你自己的域名）
/* 替换图片链接为 https */
function my_content_manipulator($content){
if( is_ssl() ){
$content = str_replace('http://www.YOUR_DOMAIN.com/wp-content/uploads', 'https://www.YOUR_DOMAIN.com/wp-content/uploads', $content);
}
return $content;
}
add_filter('the_content', 'my_content_manipulator');之前简单介绍过Tkinter：Python 可视化图形界面简单实践
这次来记点进阶心得。
Tkinter实现标签页效果
用 Python 和 Tkinter 写过一些小工具。现在想把它们整合到一起，以类似“标签页”的形式来切换。
具体参考：Tkinter 8.5 reference: a GUI for Python
用到的是 Notebook 控件，这方面网上比较少提，所以记录一下。
举例：
MyNotebook1 = Notebook(top)
MyNotebook1.place(relx=0.022, rely=0.062, relwidth=0.956, relheight=0.876)之后你就可以将 Notebook 作为 parent 来构建 Frame，承载你的标签页：
Tab1 = Frame(MyNotebook1)
....
MyNotebook1.add(Tab1, text='First tab name')与普通的 Frame 不同，完成构建的 Tab1 不是通过 pack、grid、place 来布局，而是用 Notebook 的 add 方法，并指定标签名。
再来一个例子：
#about tab
self.TabX = Frame(self.Notebook1)
self.TabXLbl = Label(self.TabX, text="Listen's Swiss Army knife")
self.TabXLbl.pack()
self.TabXLb2 = Label(self.TabX, text="ver 1.3.0")
self.TabXLb2.pack()
self.Notebook1.add(self.TabX, text='About')
#about tab end上面这个标签页实际效果大致是：
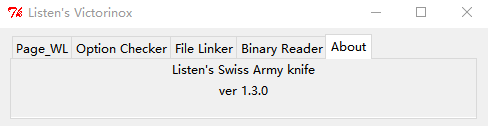
简单来说，你只要先建立了 Notebook 控件，然后往里面 add Frame 就行了，每个 Frame 都会呈现为1个独立的标签页，名字在 add 时指定。
GUI 界面与逻辑分离
如果只是一个功能简单的小工具，随便怎么写都没问题。但我在把多个小工具整合成一套时发现，东西一多了会很难管理。
在网上看到别人的做法，是将界面和逻辑分离开：
class Application_ui(Frame):
#这个类仅实现界面生成功能，具体事件处理代码在子类Application中。
def __init__(self, master=None):
Frame.__init__(self, master)
self.master.title("Listen's Victorinox")
self.master.geometry('880x380')
self.createWidgets()
def createWidgets(self):
....
class Application(Application_ui):
#这个类实现具体的事件处理回调函数。界面生成代码在Application_ui中。
def __init__(self, master=None):
Application_ui.__init__(self, master)
....上面的做法是从 TK 继承了 Frame，然后重写成自己的 UI (Application_ui)。这个 Application_ui 只生成界面，之后再用 Application 类去继承它，在 Application 里面进行逻辑处理。
单独调试 UI ：
if __name__ == "__main__":
top = Tk()
Application_ui(top).mainloop()这样的好处是，在设计 UI 时，可以只考虑控件和布局。若画面呈现不如预期，就可以直接调整。
而 UI 里的每个控件其实都是空的，它们不实现任何功能，功能都在 Application 类里去添加。
例如：
self.Tab1varWL = StringVar()
self.Tab1varWL.set("WL")
self.TabStrip1__Tab1WLNum['textvariable'] = self.Tab1varWL
self.TabStrip1__Tab1WLNum.bind("Return",self.WL2Page)self.TabStrip1__Tab1WLNum 这个控件之前是空的，现在我给它设置了 StringVar() ，并且绑定了一个事件是
Return，这个控件收到回车键时会触发 self.WL2Page 方法。另一个 tab 的实例：
# Tab4 var
self.Tab4path = StringVar()
self.Tab4pathEntry['textvariable'] = self.Tab4path
self.Tab4ButtonSelect['command'] = self.Tab4selectPath
self.Tab4ButtonConfirm['command'] = self.Tab4ReadFile相比于把 GUI 各种按钮的函数摆得到处都是，现在则可以按tab分割，都放在 Application 类的私有方法里。
对这部分进行调试：
if __name__ == "__main__":
top = Tk()
Application(top).mainloop()开发时，可以先在 Application_ui 类里面调试界面，完成后，再到 Application 类给控件们分配变量、绑定方法，验证逻辑功能。
两部分工作分割开，这样就清晰很多。制作复杂界面的 GUI 程序时，界面和逻辑的分离很有必要。
将编译好的程序打包成安装程序来发布
我在上一篇Python 可视化图形界面简单实践里介绍过，用 pyinstaller 简单快速地打包 python 程序，生成不依赖 python 的可执行文件 exe。
当时有说 -F 参数是将程序打包成一个单独的exe文件，不加则会生成一整个目录的文件。 同时也因为速度原因不建议添加这个参数。
可是程序发布时，这么多零散的文件是很不方便的，你只能将目录压缩成zip、发给别人，让别人自己去找里面的 .exe 文件。
一个合理的发布方式是提供安装文件，收到的人执行安装文件就能完成部署。
这里我们用到的工具是 NSIS（Nullsoft Scriptable Install System）。具体步骤参照这篇教程，写的很详细，我就不搬过来了：程序打包成exe文件
原则上任何语言的程序都可以这样发布。NSIS用压缩算法把你的程序那一大堆文件压成一个包，套了个安装向导的壳。
用户拿到后一运行，安装向导像所有程序一样，引导他们选择安装路径等等，然后把压缩包解压到用户路径，再为这个路径创建桌面/开始菜单的快捷方式。
NSIS 可以提供不同语言的安装向导，你甚至可以给它添加奇怪的用户协议~
这篇文章涉及的内容都是我在开发 Victorinox 小工具时遇到的。这是一把全世界只对我1个人有用的瑞士军刀。。。。。。
源码已push到GitHub：https://github.com/MamaShip/Victorinox
工作上一直使用git作为代码版本管理工具，但从来没掌握好它。最近我负责的这部分代码管理越来越混乱，掌握一套正确成熟的git工作流程几乎是迫在眉睫的事情。
git 的基础使用就不赘述了。大概每个程序员都会花几个小时掌握 git 的基础操作，再花几周去实践和熟悉吧。
首先推荐两篇文章：
- CI/CD Git Flow ： https://mritd.me/2017/09/05/git-flow-note/
- Git 工作流程 ： http://www.ruanyifeng.com/blog/2015/12/git-workflow.html
如果你没有遇到过多人协作下代码管理混乱、想要 release 新版时却交不出一份能 work 的代码，读这两篇文章可能不会很有 sense。但你只要遇过一次版本危机，再硬着头皮连续加班到凌晨一两点，回头来看就会很有感受。
上面两篇文章其实讲了2件重要的事：
- 根据你的项目性质来决定工作流（git flow / github flow / gitlab flow）
- 在一个固定模式下，git如何规范地工作
由于我在一家制造业企业，RD 只需隔一段时间 Release 一个 FW 版本给产线即可。比起敏捷地迭代，版本的稳定性更重要。传统的 git flow 是适合我们的。
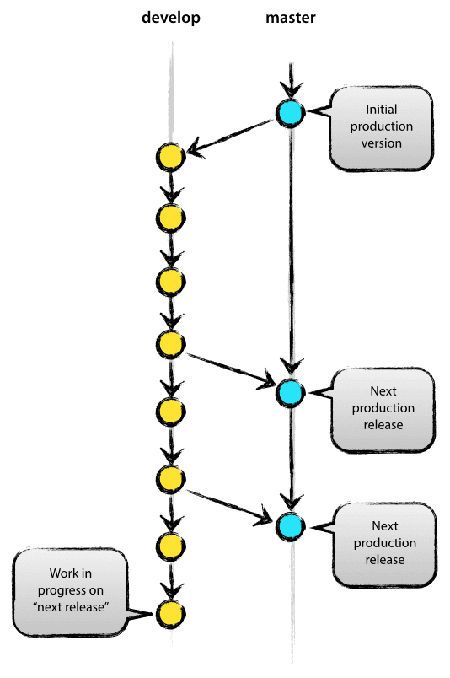
在 git flow 框架下，有2个长期分支：
- 主分支master
- 开发分支develop
master名为master，却并不是日常工作的基础分支，而是一个经过验证的稳定分支。随时可以用来发布。
与master平行存在，内容几乎相同但又略有超前的，就是develop分支。平日的开发必须基于develop分支进行。在git flow框架下，当一个新的需求产生时，你基于最新的develop拉出一个 feature/xxx 分支，进行开发，功能完成后，再合并回 develop。（合并后 feature/xxx 分支自然消亡）
3种短期分支（完成开发后，合并进长期分支，然后删除）：
- 功能分支（feature branch）
- 补丁分支（hotfix branch）
- 预发分支（release branch）
feature 只能从 develop 拉出，然后合并进 develop。
hotfix 只能从 master 拉出，然后合并进 master 和 develop。
release 则是从 develop 拉出，进行测试，完成验证后合并进 master。
当 git flow 进行 release 时，它实际做了2件事：把从上一次 release 至今的 develop 改动经过验证后合入 master，再反向把 master 合并回 develop 确保两边同步。
为什么要反向 merge 一遍，因为 release 过程中若测试出一些问题，就可以直接在 release/xxx 分支上进行修改，而这个改动是没有发生在 develop 上的。所以 release 分支在删除时会保证这些改动也被同步到develop。
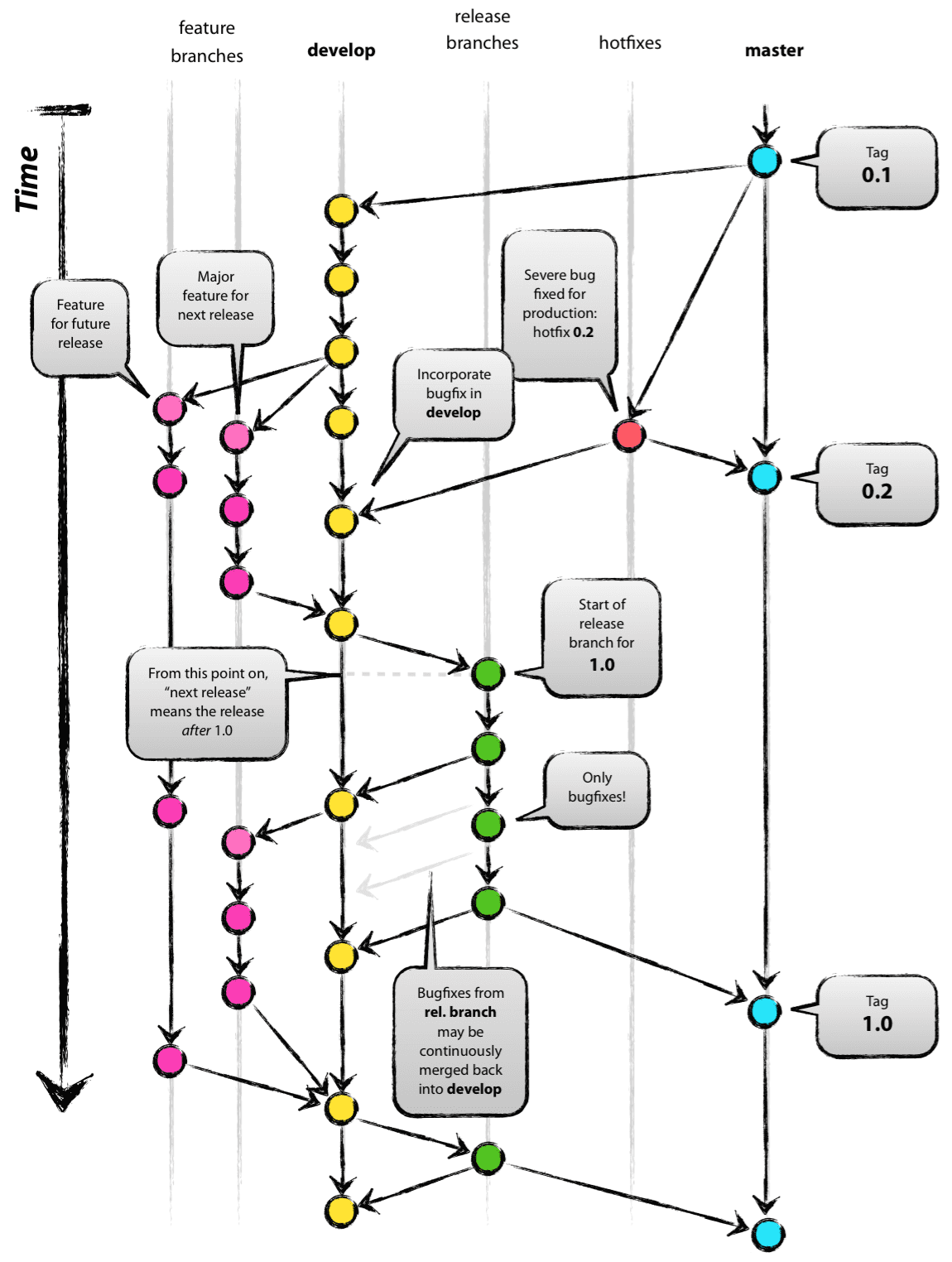
在这样的设计下，master 是稳定的，它受到 release 规则的保护，除非发生 hotfix，就只有经过测验的 release 分支才能合进 master。
而 develop 分支则相对比较敏捷，根据需求拉出 feature branch 后，开发者可以专注于自己的子任务，把兼容性等全局测试交给 release 分支去负责。
使用 git flow 相关工具，可以帮助规范这个流程。例如，工具会禁止你基于 master 拉出一个新的 feature 分支，因为新 feature 总是应该基于 develop 分支来开发，若要紧急修补某个bug，你应该使用 hotfix。
一些git flow工具（如gitflow-toolkit），还可以规范你的commit，确保commit信息清晰有效，能被script解析。这样你就能使用现成的工具（git-chglog、conventional-changelog），自动生成change log。这在 release 正式版本的时候是很有用的：
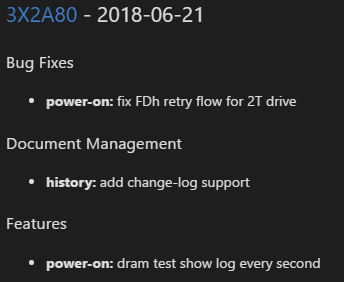
以上是我理解的 git flow 实践。在应用中发现它也对使用者提出了一些要求：
- 无论是否使用工具辅助，所有人都需要按规范格式进行commit（参考： Angular 社区规范）
- 每一项逻辑上独立的改动，应归属于一次单独的commit。
（不要在一个feature分支下进行多项任务的开发；若有多次commit都是关于同一个修改项目，应先squash再合进develop；尽量让每个 commit 都是一项独立、完整的改动，可以方便debug/release时进行cherry-pick和rebase） - git flow tool 大多是基于 Linux 系统。win下的开发者需要自我约束。
git flow 仍在实践中学习。有新的理解会再更新。