高性能计算初步：矩阵乘法

工作需要，最近在学高性能计算相关的知识。
这个领域，不涉足的时候觉得高深莫测，真正接触起来，不仅不神秘，而且十分有趣。
本文基于我对 LAFF-On Programming for High Performance （UTAustinX UT.PHP.16.01x）这门课的学习，结合个人在机器学习方面的经验总结形成，与大家分享。不当之处请指正。

如何实现高性能计算

从字面上来说，算得快就是高性能计算。
以此为定义，拥有超级计算机是做高性能计算的第一步，因为它从硬件性能上支持了「high performance」。
但显然，「硬件快」只是「high performance」的一个组成部分。在有限的硬件性能下，还有方法可以算得快。
例如分布式和并行化：把任务拆分成可以并行执行的多个部分，用多台机器同步运算，是个好主意。
或者给机器上插很多块显卡（GPU），利用显卡的并行计算能力，来做异构计算（由CPU执行串行部分，GPU执行并行部分）。
——如果只有一台机器，没有显卡，机器的性能也很一般呢？

本文接下来要讨论的，就是在常规架构的普通计算机单机上，如何做高性能计算编程。
特殊地，我们讨论最常用的一种运算：矩阵乘法。我们将会看到，它在时下流行的神经网络中如何被广泛应用，又是如何被最高效地实现为C代码。

关于IO的思考

数据在存储介质间的 IO 对实际运算速度有巨大影响。

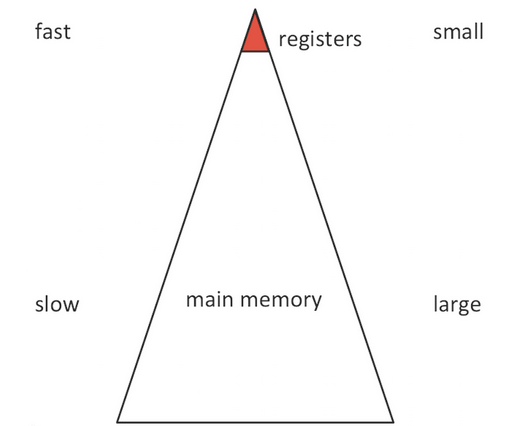
如果以简化模型来看，单是内存 <---> 寄存器之间：

一份数据，在内存和寄存器间传输，比 CPU 执行运算，耗时要高出2个数量级（100倍以上）。

——这一差距随着集成电路技术的发展被继续拉大。

如果认为花在计算上的时间是有效开销，花在IO上的是无效开销，基于上面的事实，可以做出一个粗略估计：

若想让IO瓶颈被掩盖，每次数据读入 register 都要执行100次以上运算再输出，才能有效利用 CPU。

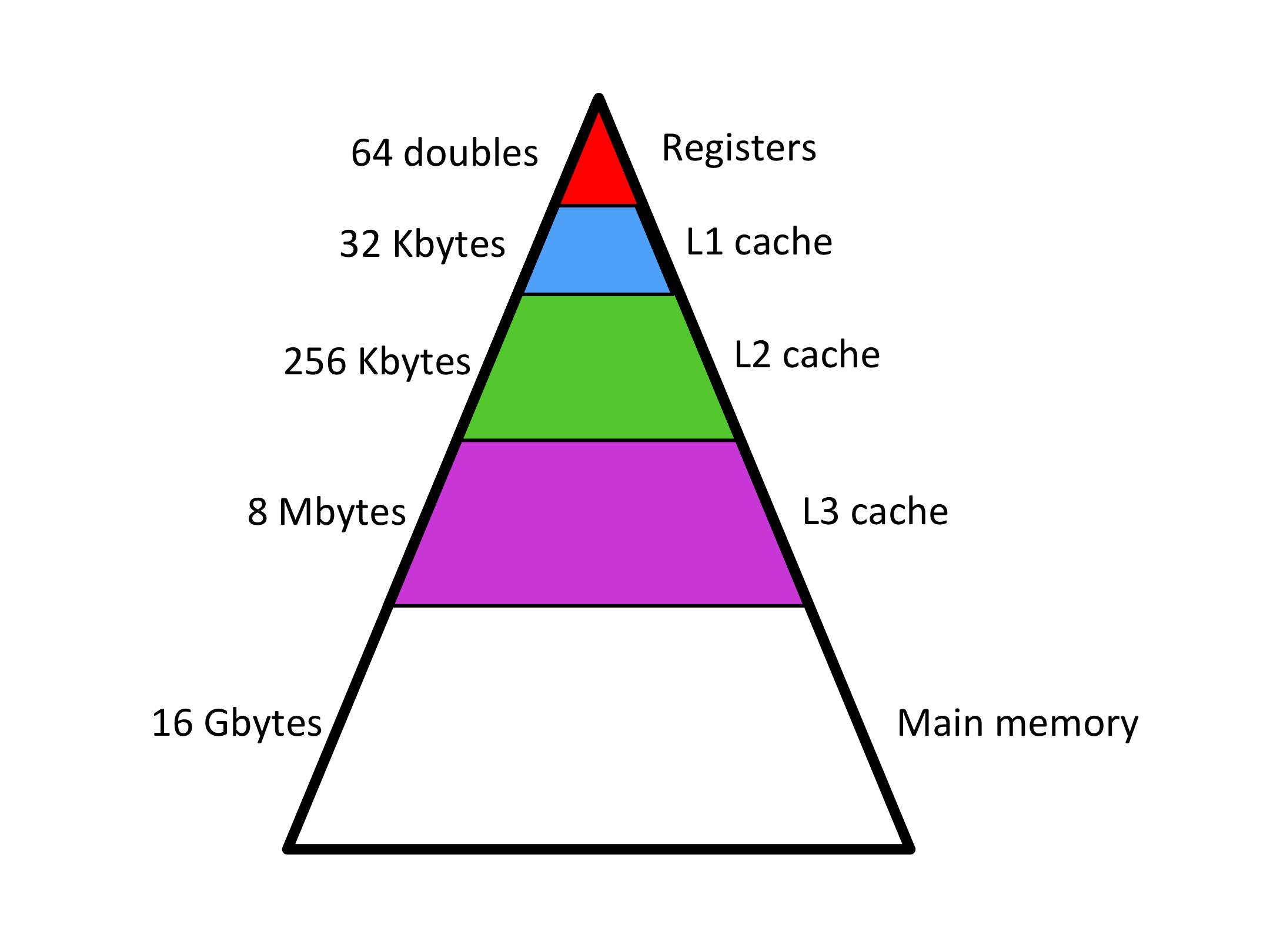
在当下典型的计算机架构中，内部存储的层级可以包含：

• 寄存器（register）
• 多级缓存（caches）
• 主存（内存，main memory）

它们的容量依次增大，但传输速度递减。
把数据IO耗时简化为100倍看来是过于草率了，因为 data 会被预载进 cache 中，来加速调用过程。
对缓存的精细控制，也是接下来要讨论的重点之一。

本文将要讨论高性能运算编程的一个关键命题：

如何足够精明地调度资源，充分挖掘各级缓存的潜力，使运算高度集中在选定的数据单元上。
从而使计算性能被真正用在数据计算上，而不是数据IO。

神经网络中的矩阵运算

机器学习领域有很多数学运算，而深度学习向来被视为一种大规模密集型运算的场景。其中很多网络结构都可以被表示为矩阵运算，从而实现并行化的快速训练和推理。

以全连接层为例。我们知道，最小的运算单元是感知机（perceptron）：

接受一个输入x，线性变换后输出y，公式在右侧给出。

更进一步，如果要形成网络，感知机之间会有更多的连接：

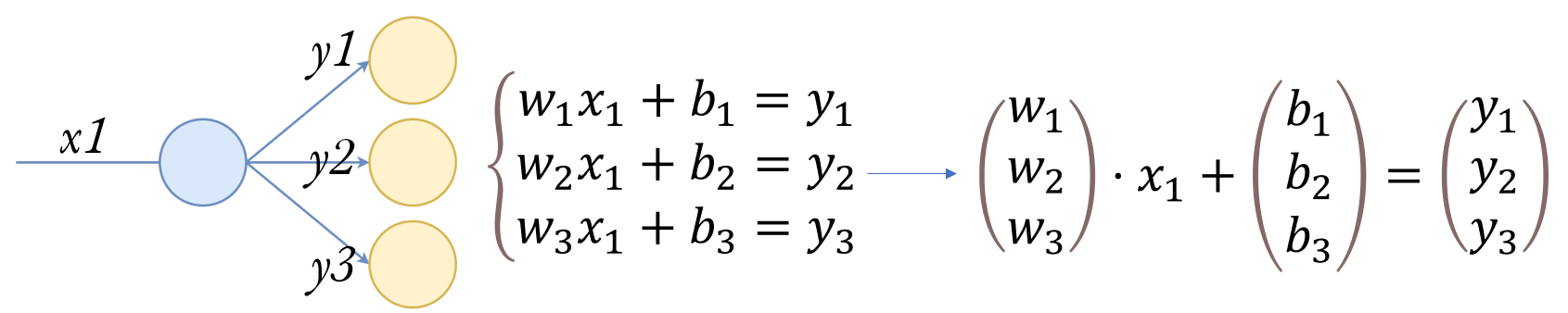
假设此时的1个输入 x1，对应了3个输出 y1，y2，y3。
可以写出3个线性变换公式，形成了一个方程组。我们发现方程组的形式可以直接用线性代数里的符号表示，写成上图右侧的形式
因此该网络结构就被表达成了：

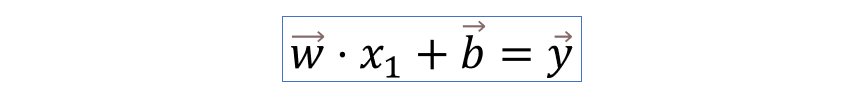
继续，全连接层的普通形式：

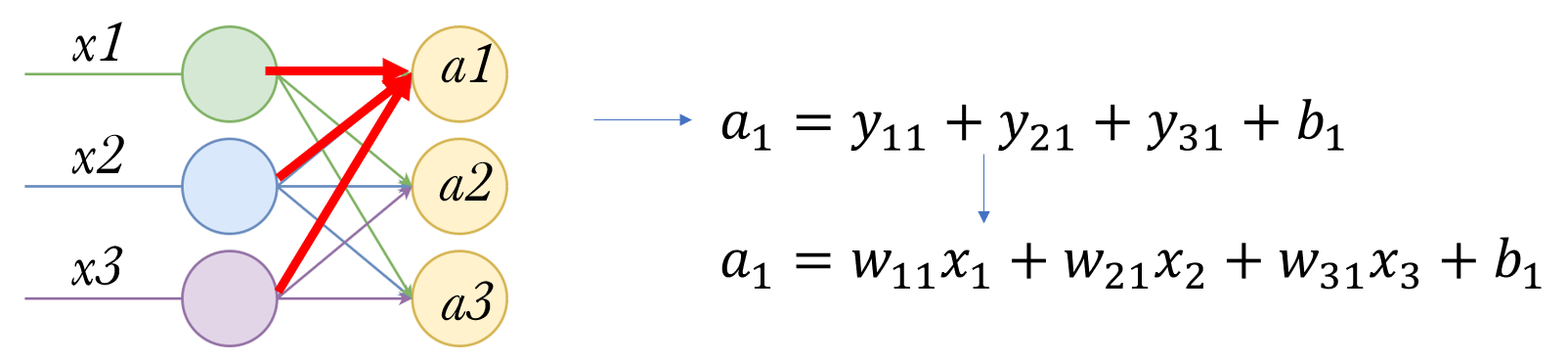
先关注其中一个输出 a1，它由3条连接决定，分别是上一层三个感知机的输出。
由于3条连接上的偏置量 b 可以合并同类项，所以直接写成一个 b1。那么 a1 的计算就由右边的式子给出。

同理可以列出方程组：

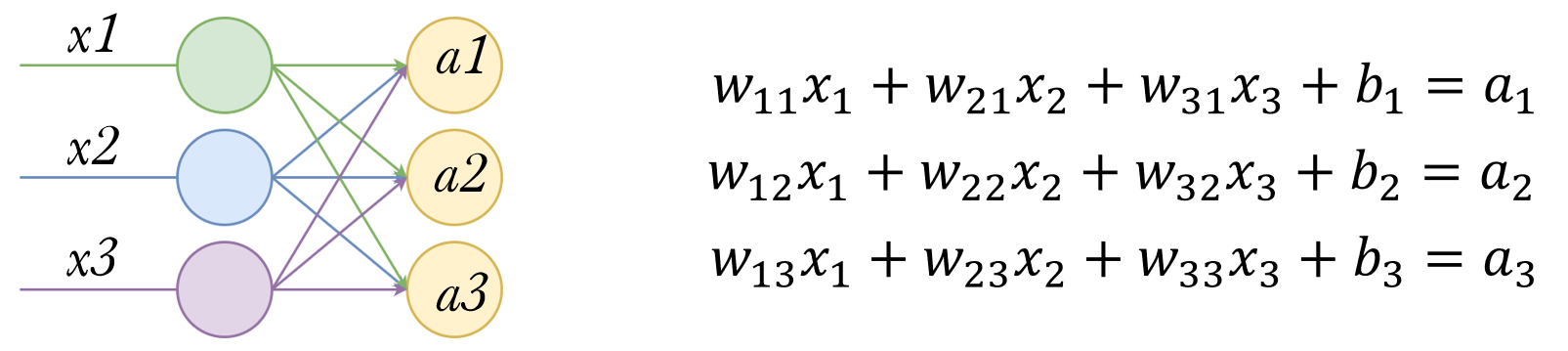
写成矩阵形式：

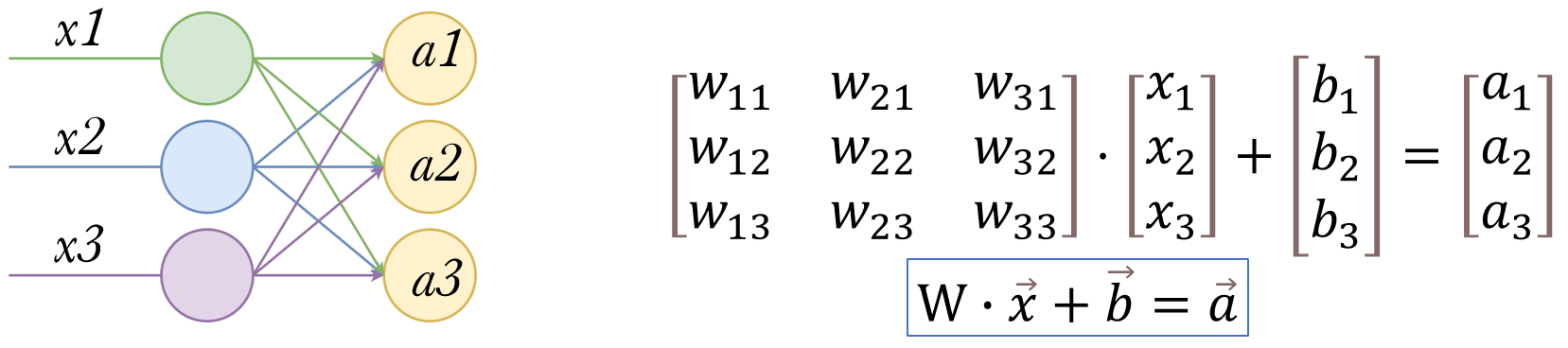
至此全连接层就完全由矩阵和向量的运算表达了出来。

它不像软件工程领域里，编写一个类（class）叫「感知机」、为这个类生成大量的实例对象、把它们连接起来形成网络……——那样太低效了。
全连接层实际只用一个线性代数公式就实现了。简洁又快速，在 Matlab 里只需要一行代码。
可以看出，最终得出的线性变换，在形式上与最初感知机的公式是一致的。都是输入x，乘上权重w，加偏置量b，得到输出。

以上我们只讨论了全连接层如何使用矩阵运算展开，如果对卷积层的矩阵实现感兴趣，可以参考这篇文章：Why GEMM is at the heart of deep learning。
实际网络中，不止会用到卷积层和全连接层，还会有激活函数等等。但激活函数的运算开销是非常小的，从贾扬清当年的论文里可以看到，神经网络最耗时的部分基本都在卷积层。而卷积层里就是在做大量的矩阵乘法。

矩阵乘法的实现

C = AB

朴素版本

按矩阵相乘的定义，C 矩阵中位于 i，j 的元素，由 A、B 中相应 行×列 累加得来。
经过三层循环，遍历 C 的所有位置，并做 k 次累加得出最终结果：

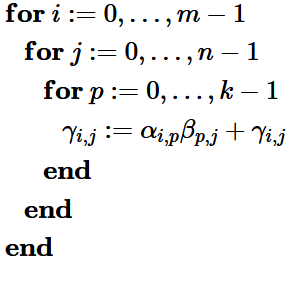
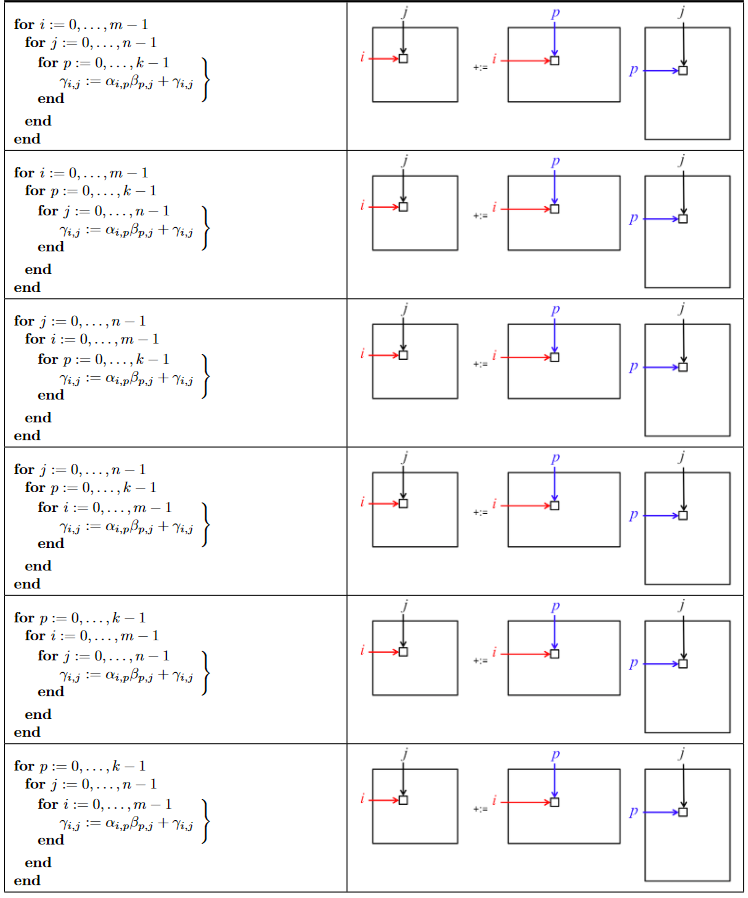
你会发现：诶，反正最内层的计算是独立的，改变这些循环的顺序并不影响最终结果，所以你也可以选择最外层先 for p，也可以先 for j
——三层循环的顺序可以任意调换，而最终结果相同。

那我们交换它们的顺序看看，i j p 排列组合，共6种可能性：

用这些版本计算各尺寸的矩阵，将计算效率以 GFLOPS 表示

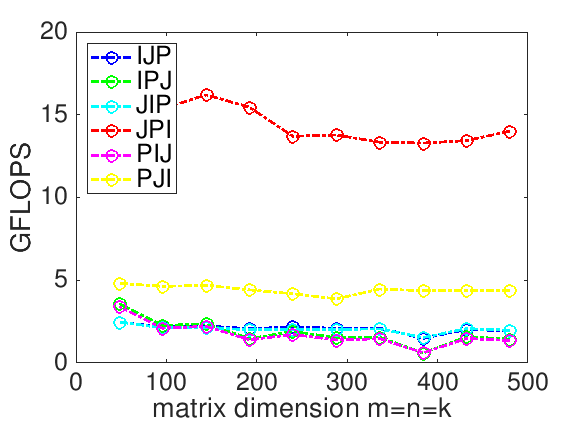
你会发现计算顺序改变居然给计算效率带来了3~4倍的变化。

图上最快的 JPI 就是矩阵运算的最佳实践吗？

如果用 BLAS 库来执行相同的运算，把运行效率画在图上（Ref这条线），就比 JPI loop 还要快 5 倍

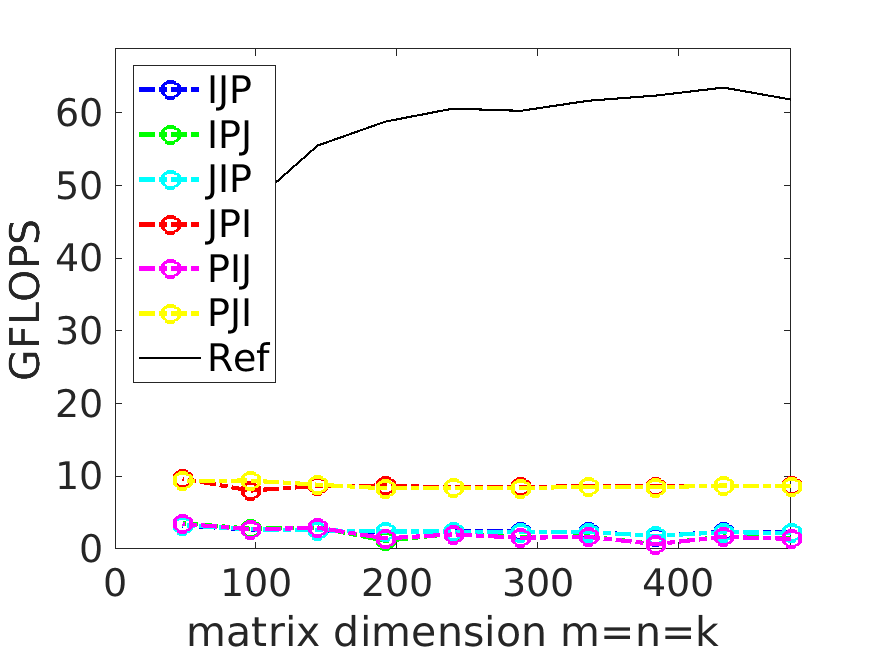
为什么会这样？
因为矩阵数据在内存中是连续存储的。当我们用三层循环遍历这些数据做计算时，某些遍历顺序可以最大化地连续访问相邻地址。
这些连续访问，极大地受益于CPU的缓存、分页和预取（prefetch）。使得一次读取操作就能支持后面的多次运算。

这些在我们无意识中发生的优化，带来了显著的性能差异。而如果我们人为地编织运算过程，使所有这些优势都被利用起来，就能实现最佳性能（Ref那条线），也就是 BLAS 运算库所实现的版本。

关于朴素矩阵乘法的细节，有人已经把课堂内容做了更详细的总结，可以参考他的文章：《高性能计算简介（一）：初步分析，BLAS，BLIS简介》

迈出一小步：分块矩阵

朴素版本还有一个问题，是面对大矩阵时性能明显下降。
当矩阵大到无法被缓存容纳时，遍历连续内存的各种优势就都消失了，朴素版本的性能会急剧下跌。

这让我们回想起线性代数课上的知识：分块矩阵
当矩阵乘法的数据量和运算量都超出当前计算机架构能有效处理的范畴，我们就把它拆分成子任务来执行——分块矩阵乘法。

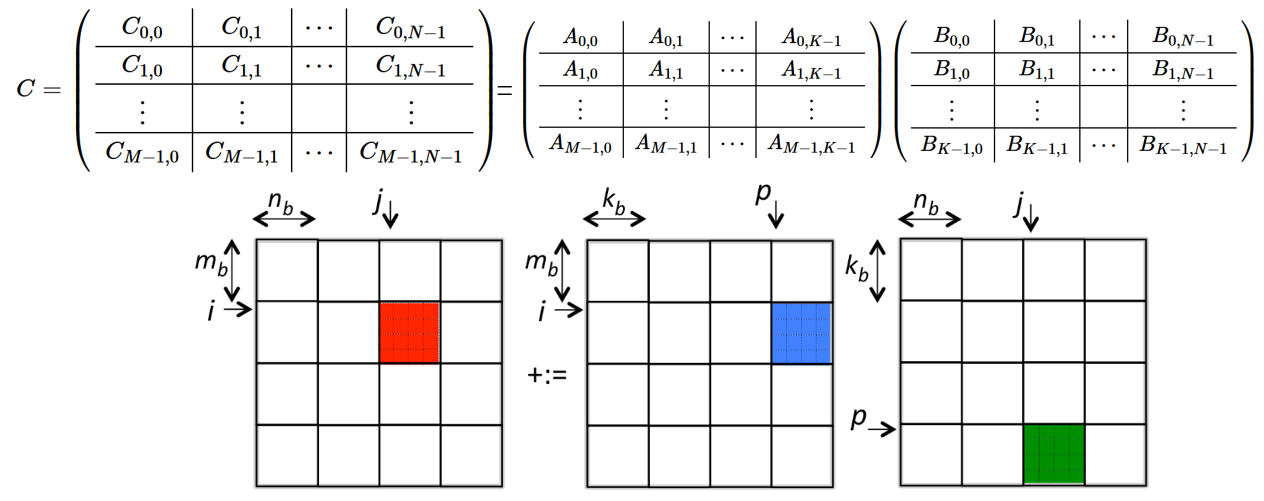
如上图所示，C 矩阵可以被切分成形如 C1,2 这样的小矩阵，A、B矩阵也做相应的切分，则运算被缩减为每次只关注三个小矩阵的运算。

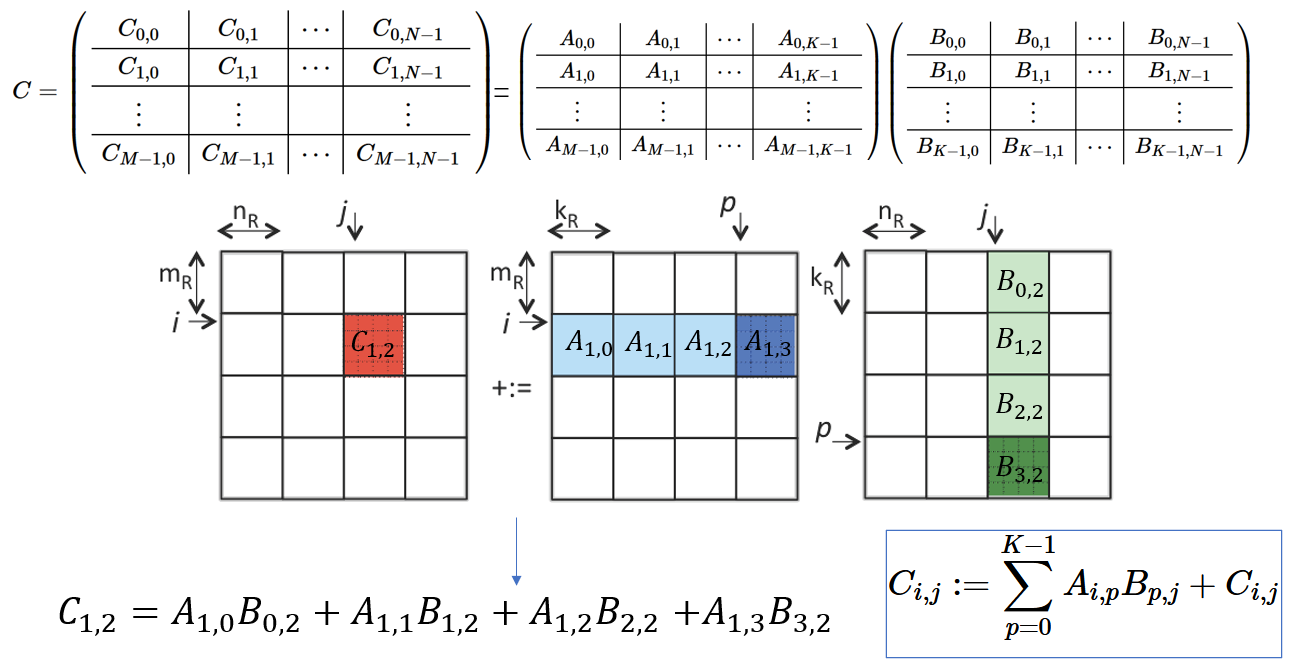
例如计算 C1,2 矩阵，就由 A 中的4个小矩阵与 B 中的4个小矩阵分别相乘，然后累加得出。
总结成一般规律，即为上图方框内的公式。

很好，我们迈出了一小步，成功把问题分解为一个看起来一模一样的子问题。同时还缩小了问题的规模。

矩阵乘法的子操作

分块后的矩阵相乘仍然是矩阵乘法，它的复杂度还是很高。从数学的角度来看，还可以继续细分。

让我们有请矩阵与向量乘法~

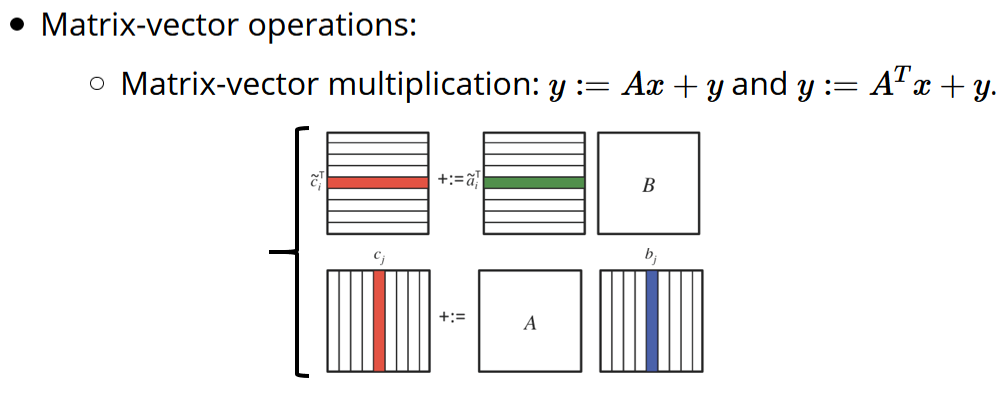
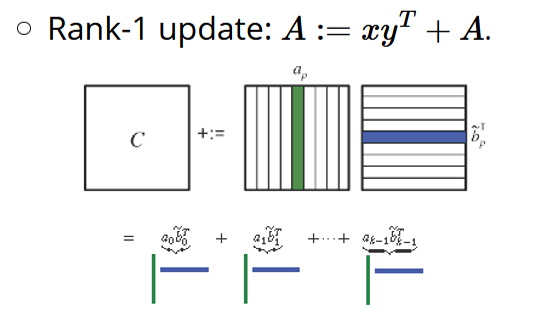
向量相乘累加计算矩阵的 Rank-1 update~

以及，似乎不必画图解释的向量间运算：点乘，和axpy（向量x乘scalar缩放后，再加向量y）

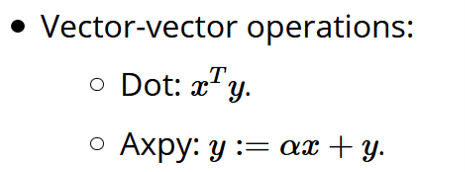
有了这些「子操作」，我们得以继续拆分矩阵乘法，把它拆成了矩阵和向量之间的运算、向量和向量之间的运算。这样我们就有了更细粒度的操作可以进行调度了。

分块矩阵，我是你的破壁人

有了上面的「子操作」，我们可以把矩阵相乘再细分成向量乘法（以 Rank-1 update 为例）

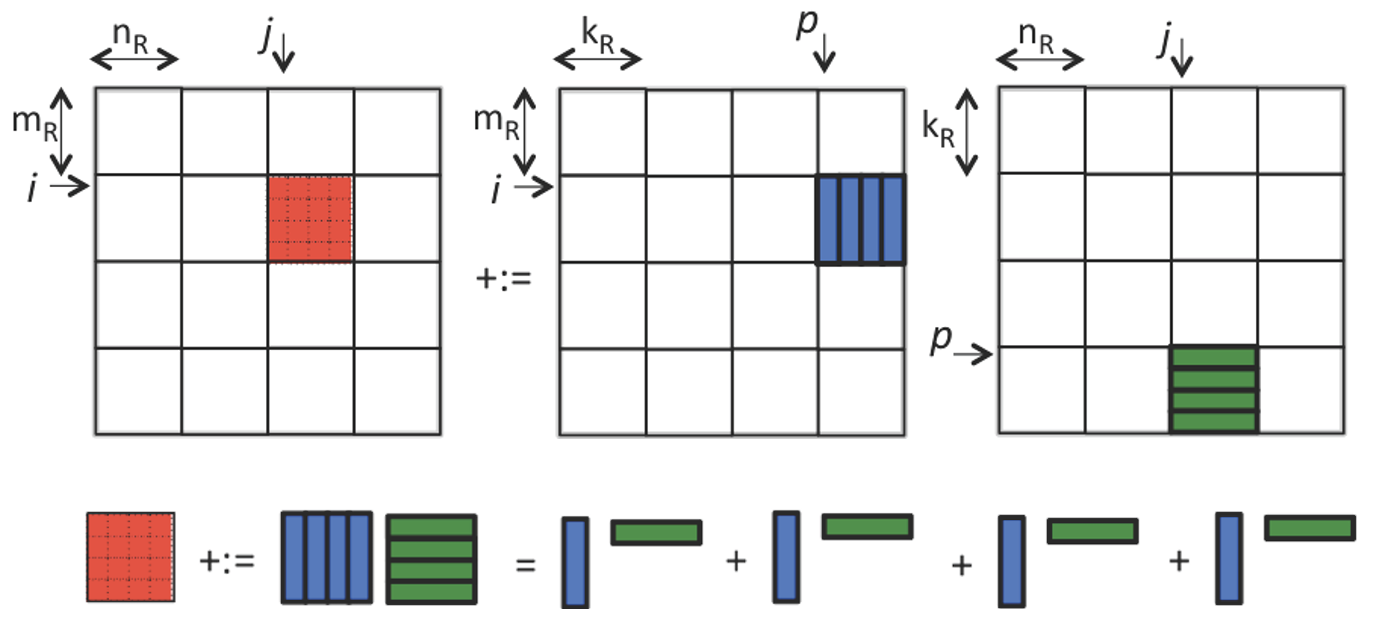
那么我们就不必把整个小A矩阵和整个小B矩阵都装载进缓存。
而可以每次只读取它们的一个列向量和行向量，执行计算，更新（update）到C矩阵，再循环累加。

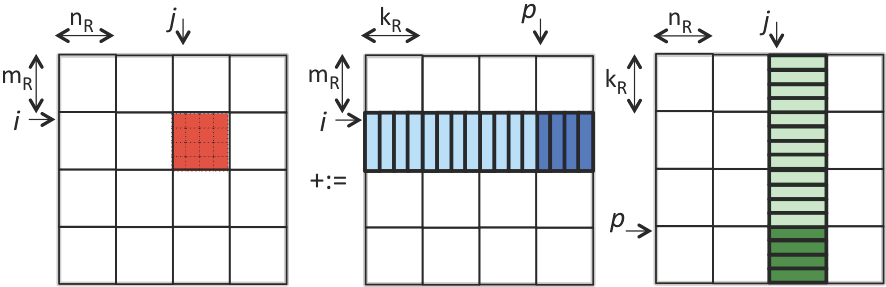
从「把数据装载进缓存」的角度思考，「分块矩阵」的概念也被打破，只有C矩阵是被分「块」（micro-tile）来处理，A、B矩阵实际被分为「条」(micro-panel)

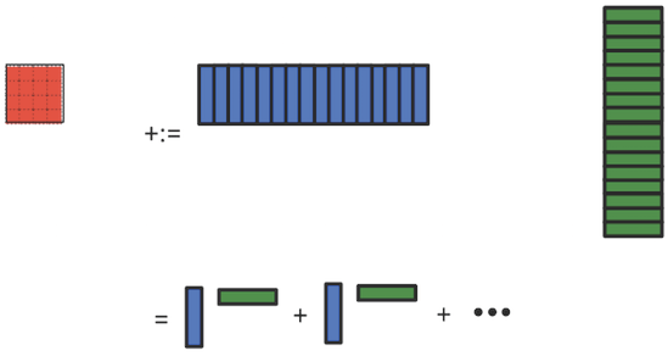
每「条」数据中再拆分出 𝑎 ⃗𝑖、𝑏 ⃗𝑖 向量，轮流加载进寄存器，相乘之后做 rank-1 update

核函数编程

最酷的部分来了。
我们有了丰富的拆分手段，而每次拆分时都可以选择不同的 sub_size 来调整子操作大小。
但把「子操作」拆分到多小是让人满意的呢？不妨看看你的计算机支持什么运算吧！

Micro-kernel

以 Intel CPU 为例

Intel AVX2 指令集，支持 vector register 中同时存储 4 个 double 型。
对它们下发一个指令，就可以同时对4个数据做运算。
（这就是SIMD，单指令多数据流）

考虑到 Intel CPU 最多也只能做到这样了。
所以我们可以把最小运算设定为上图，4×4 的小C矩阵，通过不断累加更新，由A和B中拆出的小向量（长度为4）相乘计算得出。

代码实例

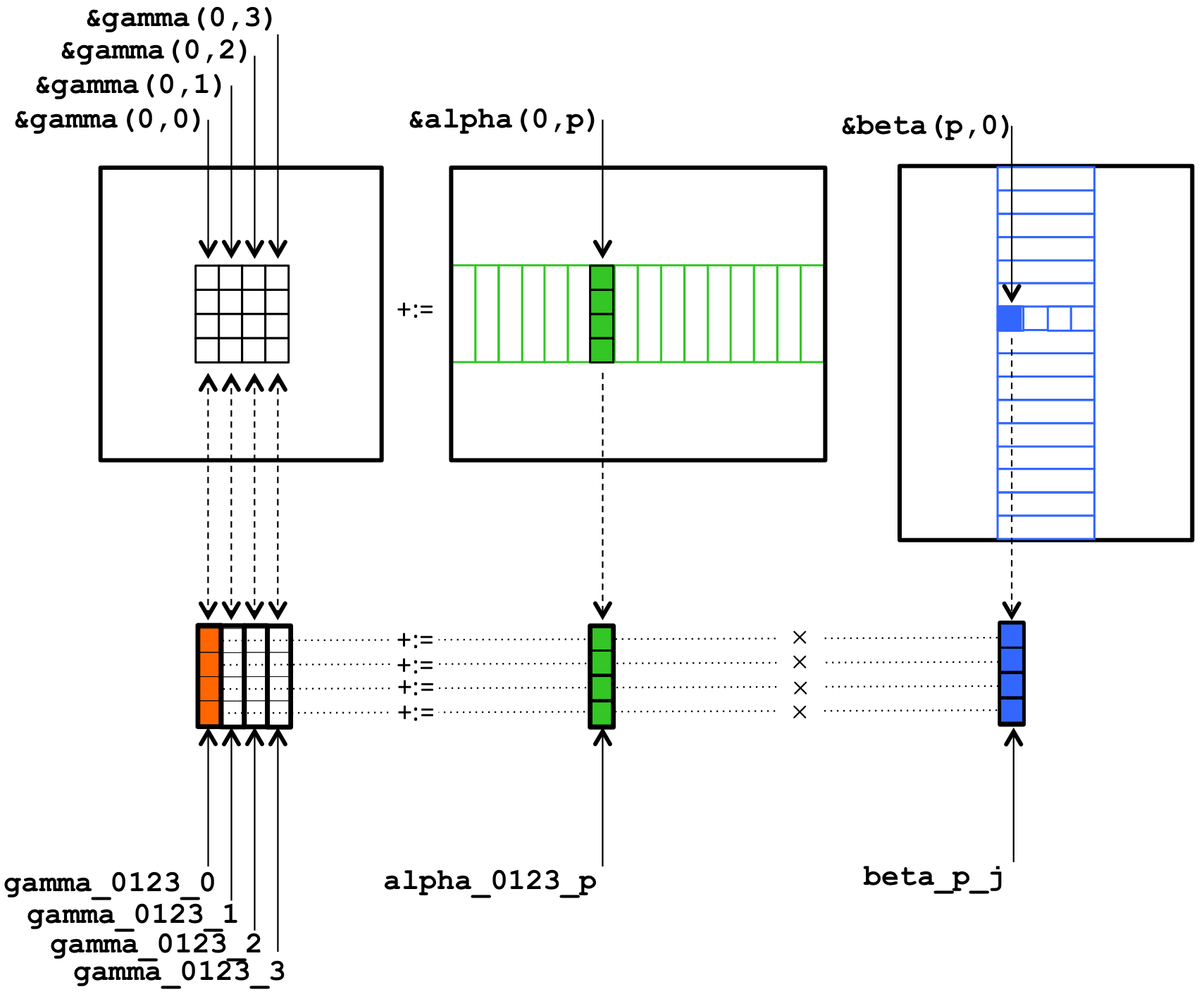
使用 Intrinsic function（由编译器提供）获取「寄存器变量」（如图）。

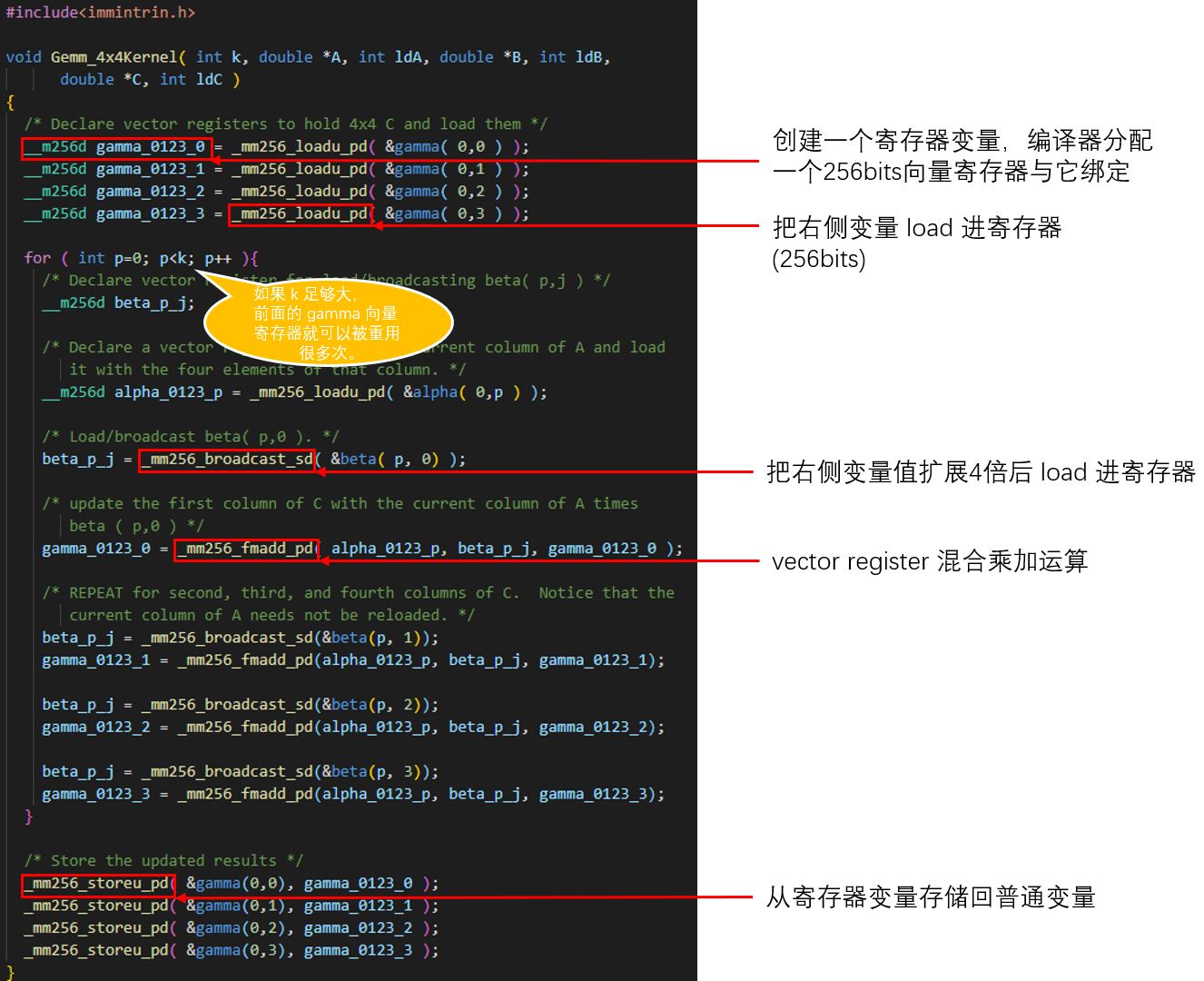
对寄存器变量的操作就直接对应到寄存器运算。

得以显式地将我们认为最高频的计算量常驻在寄存器内。

从图上也可以看到，小C矩阵中的相关数据在 kernel 循环开始前就 load 进了寄存器，在之后的 k 次循环中重复使用（被累加）。
只要这个 k > 100，就满足了文章开头我们的假设：数据一次装载（IO）对应了 >100 次运算。

实际应用中，矩阵尺寸往往都很大，所以这个条件很容易满足。

运算的顺序决定了如何触发缓存

如果忽略 packing 之类的内存优化细节（它们在矩阵不够大的时候引入了不可忽视的额外开销），我们已经离终点很近了。

前面的工作使我们能够把「矩阵乘法」分解为不同粒度的一些子运算。而它们的执行顺序是可以调度的。
你的调度方式决定了数据访问顺序和频率，从而触发并利用了 CPU 的缓存机制。

假设这一系列运算以下面的顺序执行：

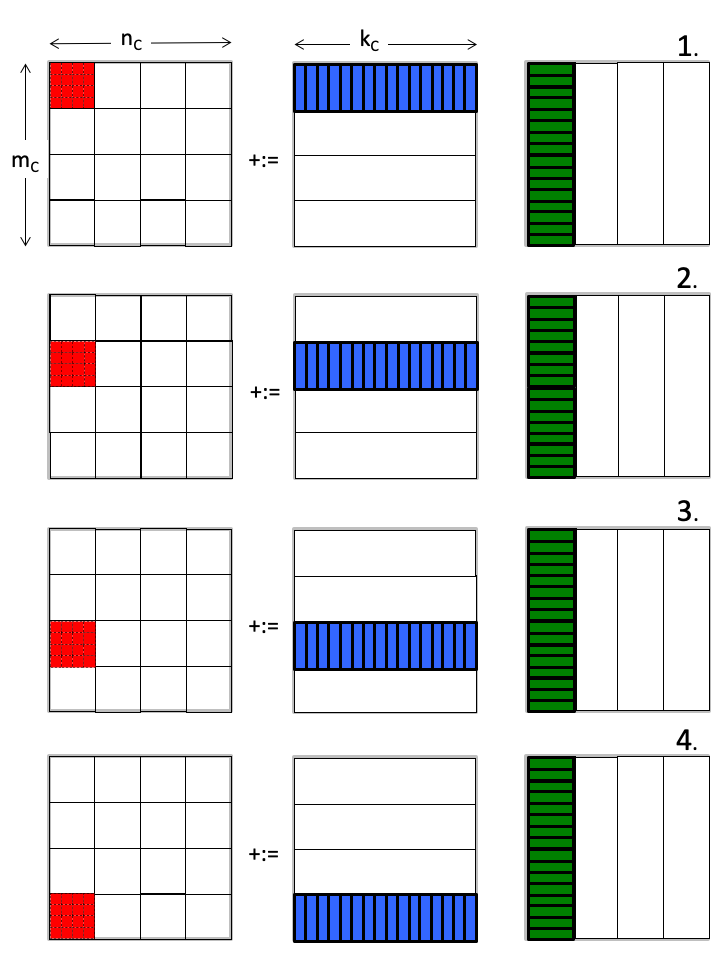
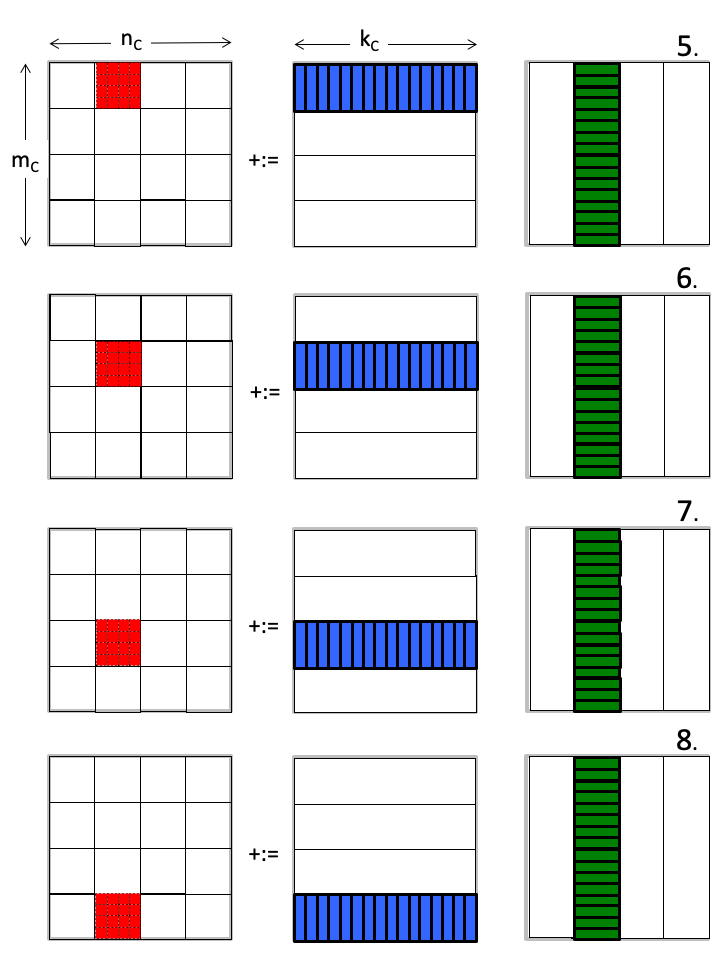
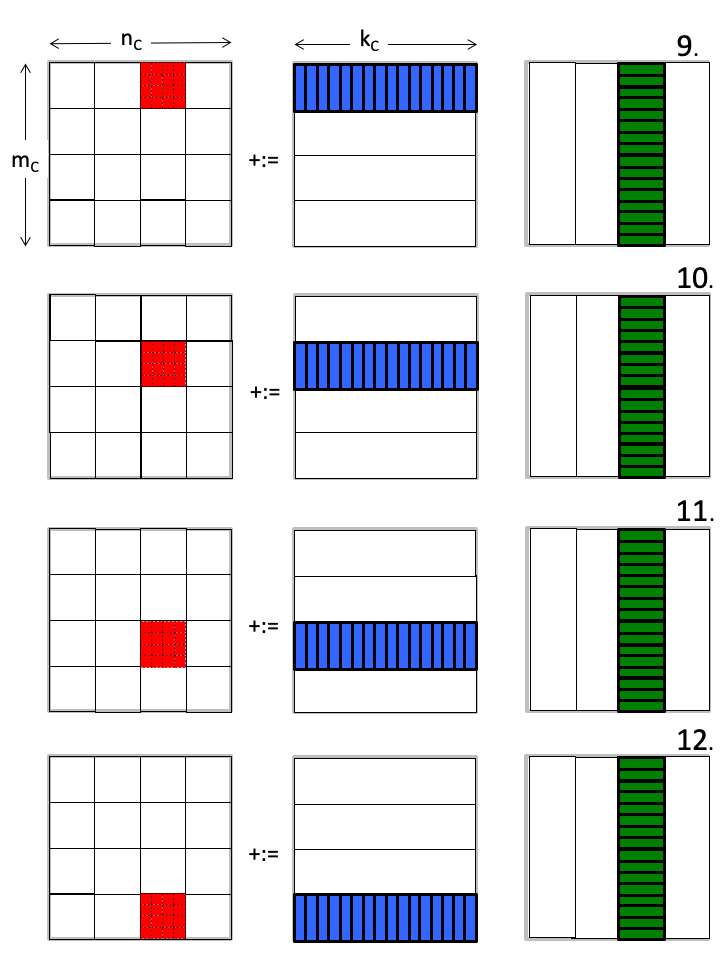
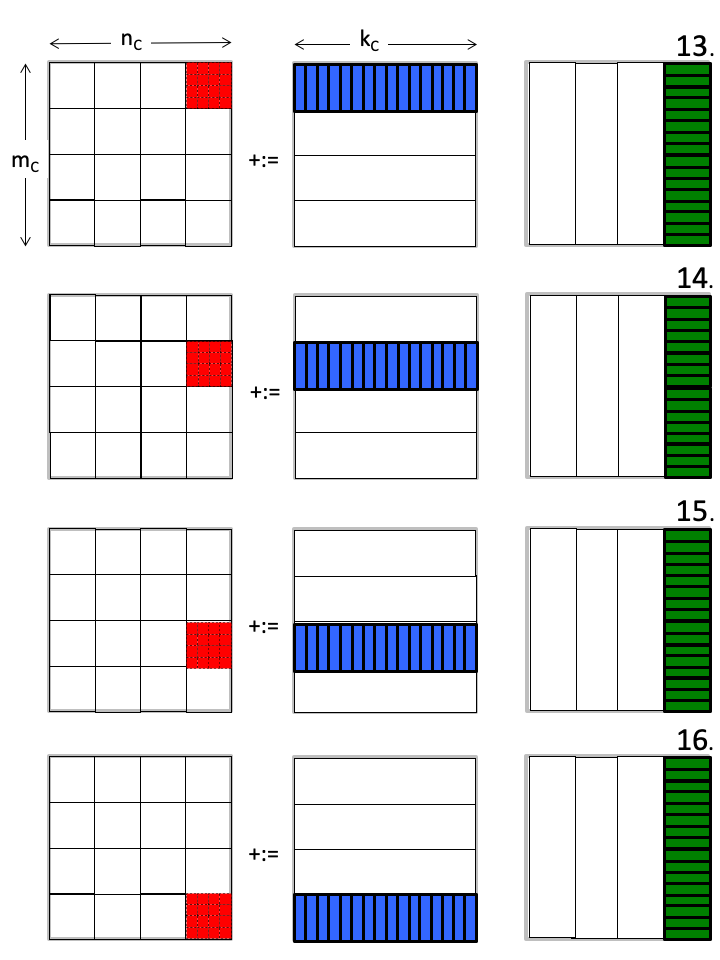
你发现了什么？

C 矩阵里每次聚焦于一小块区域（micro-tile，红色），密集地「更新」它里面的数据，直到全部计算结束，写回内存，就不再需要二次访问。
B 矩阵里的 micro-panel（绿色），虽然没有被频繁使用（每次只用到里面一个行向量），但却被相邻的 C 子矩阵重复使用。
A 矩阵里的 micro-panel（蓝色），切换的很频繁，但每次装载之后都进行了大量的运算（细节在 micro kernel 的运算里）。

有想法了吗？再回顾下这个图

我觉得：从B矩阵切分的 micro-panel 应该整块被放在 L3 cache，而A矩阵的 micro-panel 最好能被切块后轮流加载进 L2 cache，最小的运算单元 4×4 C矩阵则应该直接常驻在 Register 里，正如我们 kernel 函数里实现的那样。

5 loops

整理上述过程，我们最终获得一个由5层循环组成的计算步骤：

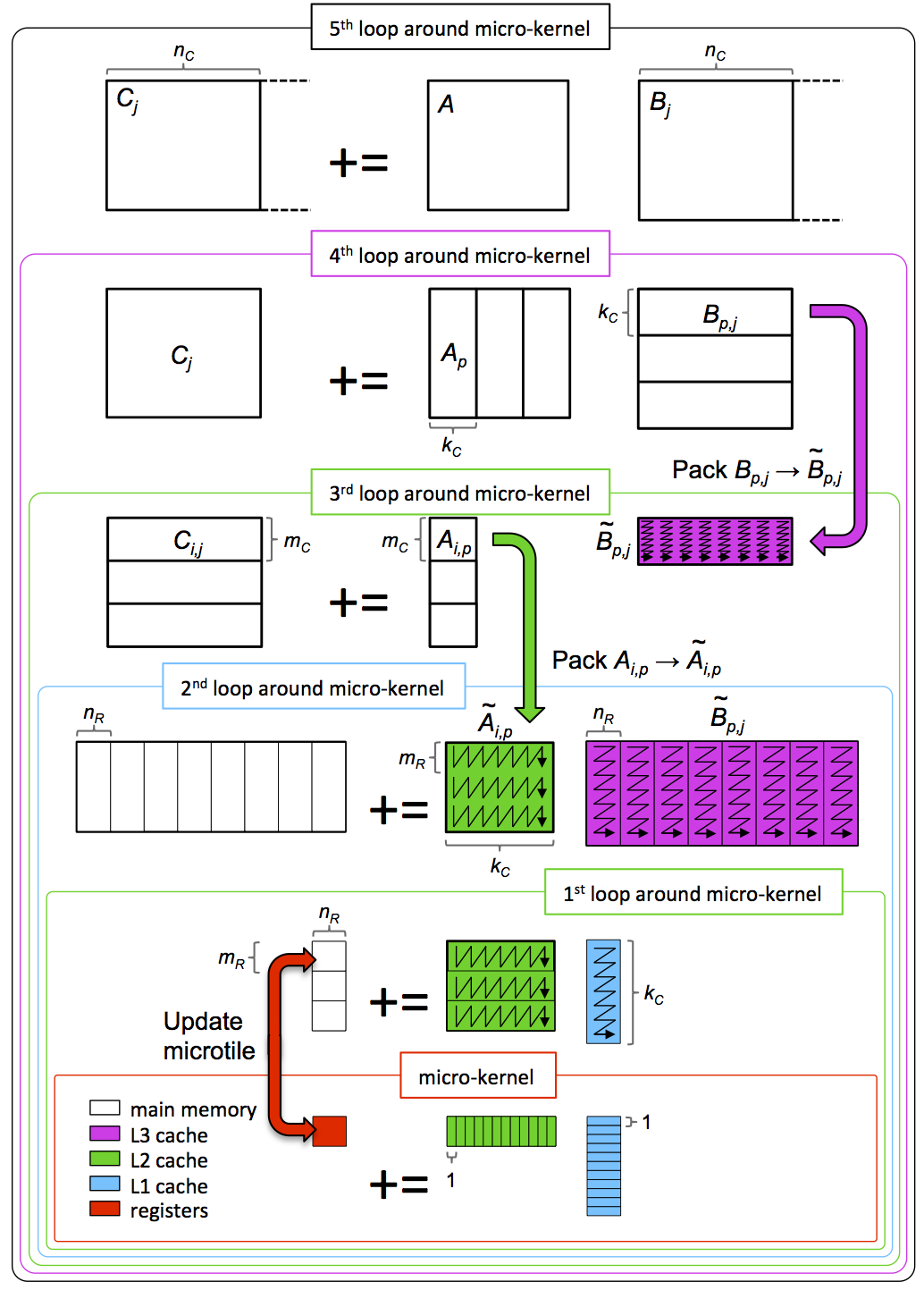
我们不能用命令来控制 CPU 把哪些数据 cache 到哪里。但基于对所用计算平台的理解（架构理解），通过明智地选取各 loop 层级数据块的大小，并调整它们的计算顺序来触发 cache，最终可以「骗」CPU 把我们设想的部分存到对应的缓存里（*图中数据颜色对应目标缓存层级的颜色），实现对寄存器和缓存的高效利用。

这就是 BLIS 运算库（基于 GotoBLAS2 改进而来）2017年的算法实现。

总结

上述矩阵乘法的高性能运算思想，最早由日本的 Kazushige Goto 提出。发表在这两篇论文里：

• Kazushige Goto and Robert van de Geijn, On reducing TLB misses in matrix multiplication, Technical Report TR02-55, Department of Computer Sciences, UT-Austin, Nov. 2002.
• Kazushige Goto and Robert van de Geijn, Anatomy of High-Performance Matrix Multiplication, ACM Transactions on Mathematical Software, Vol. 34, No. 3: Article 12, May 2008.

因而被称为 Goto’s algorithm 或 GotoBLAS algorithm （因为他把方法应用在 BLAS 运算库上，编写了当时领先的开源矩阵运算库 GotoBLAS）

全文只讨论了单核运算的场景。该算法用单核吃尽了所有缓存资源，实现单核最高效的运算版本。
如果有多核可以并行执行运算，则要考虑它们共用L3缓存（但又有各自的L2、L1缓存）时资源竞争和隔离的状况，重新设计调度方式。

我刻意避免了中间的数学证明过程，和理论极限的计算方法。有兴趣的同学可以自己去上这门 MOOC 探究细节。

除了内存 packing 技术和 Strassen algorithm，本文几乎涵盖了高性能计算编程的基本工作方法:
将任务拆分为多种不同粒度的子任务、基于架构去调度这些任务使它们最大化利用计算资源、使用核函数编程来精细地操作数据……

要将这些方法扩展到其他领域也不难。例如在 GPU 上用并行编程实现矩阵乘法的高性能版本：

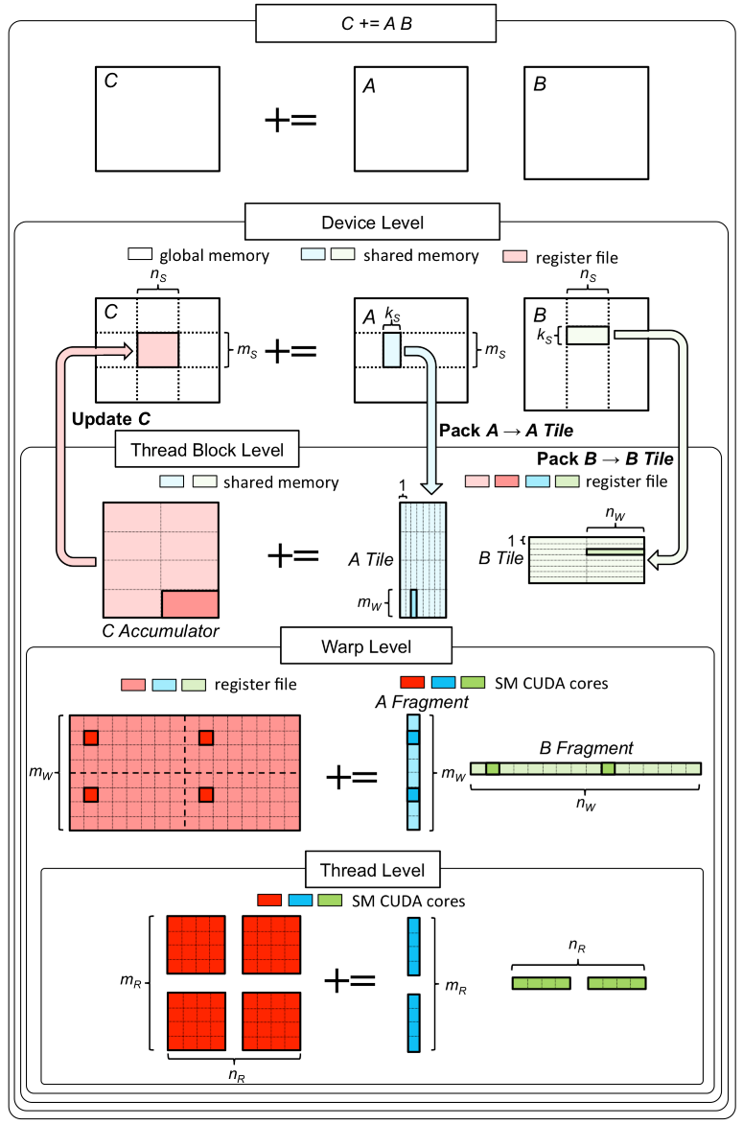
也是用5层 loop 拆分，只是拆分方式要考虑到最大化地并行执行，使所有 SM 在有限的资源下被利用。
具体可以看 Nvidia 官方文章：CUTLASS: Fast Linear Algebra in CUDA C++

GPU 高性能编程也是我接下来要学习的方向，如果有更多理解，我会再分享出来。